Decoding the math behind Diffusion Models: A breakthrough in Generative AI

Diffusion models are a new class of state-of-the-art generative models that generate diverse high-resolution images. There are already a bunch of different diffusion models that include Open AI’s DALL-E 2 and GLIDE, Google’s Imagen, and Stability AI’s Stable Diffusion. In this blog post, we will dig our way up from the basic principles described in the most prominent one, which is the Denoising Diffusion Probabilistic Models (DDPM) as initialized by Sohl-Dickstein et al in 2015 and then improved by Ho. et al in 2020.

Images produced by Dall-E 2

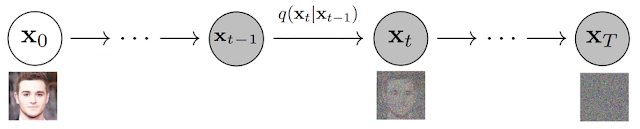
The basic idea behind diffusion models is rather simple. It takes an input image $\mathbf{x}_0$ and gradually adds Gaussian noise to it through a series of $T$ time steps. We will call this the forward process. A network is then trained to recover the original image by reversing the noising process. By being able to model the reverse process, we can start from random noise and denoise it step-by-step to generate new data.

Forward Diffusion Process

Consider an image $\mathbf{x}_0$ sampled from the real data distribution (or the training set). The subscript denotes the number of time step. The forward process denoted by $q$ is modeled as a Markov chain, where the distribution at a particular time step depends only on the sample from the previous step. The distribution of corrupted samples can be written as, \begin{align*} q(\mathbf{x}_{1:T} | \mathbf{x}_0) &= \prod_{t=1}^T q(\mathbf{x}_{t} | \mathbf{x}_{t-1}) \tag{1} \end{align*}

At each step of the Markov chain, we add Gaussian noise to $\mathbf{x}_{t-1}$ producing a new latent variable $\mathbf{x}_t$. The transition distribution forms a unimodal diagonal Gaussian as, \begin{equation*} q(\mathbf{x}_{t} | \mathbf{x}_{t-1}) = \mathcal{N} (\mathbf{x}_t; \; \mu_t = \sqrt{1 - \beta_t} \; \mathbf{x}_{t-1}, \; \Sigma_t = \beta_t \mathbf{I}) \tag{2} \end{equation*} where $\beta_t$ is the variance of Gaussian at a time step $t$. It is a hyperparameter that follows a fixed schedule such that it increases with time and lies in the range $[0, 1]$.

Ho et al. sets a linear schedule for the variance starting from $\beta_1 = 10^{-4}$ to $\beta_T = 0.02$, and $T = 1000$.

A latent variable $\mathbf{x}_t$ can be sampled from the distribution $q(\mathbf{x}_{t} | \mathbf{x}_{t-1})$ by using the reparameterization trick is as, \begin{equation*} \mathbf{x}_{t} = \sqrt{1 - \beta_t} \; \mathbf{x}_{t-1} + \sqrt{\beta_t} \; \epsilon_t \tag{3} \end{equation*} where $\epsilon_t \sim \mathcal{N}(0, 1)$.

Equation 3 shows that we need to compute all the previous samples $\mathbf{x}_{t-1}, ..., \mathbf{x}_{0}$ in order to obtain $\mathbf{x}_t$, making it expensive. To solve this problem, we define, \begin{align*} &\alpha_t = (1 - \beta_t), &\bar{\alpha_t} = \prod_{s=0}^T \alpha_s \end{align*} and rewrite equation 3 in a recursive manner, \begin{align*} \mathbf{x}_{t} &= \sqrt{\alpha_t} \; \mathbf{x}_{t-1} + \sqrt{1 - \alpha_t} \; \epsilon_t \\ &= \sqrt{\alpha_t} \; \left[ \sqrt{\alpha_{t-1}} \; \mathbf{x}_{t-2} + \sqrt{1 - \alpha_{t-1}} \; \epsilon_t \right] + \sqrt{1 - \alpha_t} \; \epsilon_t \\ &= \sqrt{\alpha_t \alpha_{t-1}} \; \mathbf{x}_{t-2} + \sqrt{ (\alpha_t)(1 - \alpha_{t-1}) + (1 - \alpha_t)} \; \epsilon_t \\ &= \sqrt{\alpha_t \alpha_{t-1}} \; \mathbf{x}_{t-2} + \sqrt{1 - \alpha_{t} \alpha_{t-1}} \; \epsilon_t \\ & ... \\ &= \sqrt{\alpha_t \alpha_{t-1} \; ...\; \alpha_{0}} \; \mathbf{x}_{0} + \sqrt{1 - \alpha_{t} \alpha_{t-1} \; ... \; \alpha_0} \; \epsilon_t \\ &= \sqrt{\bar{\alpha_t}} \; \mathbf{x}_{0} + \sqrt{1 - \bar{\alpha_{t}}} \; \epsilon_t \tag{4} \end{align*}

The close-form sampling at any arbitrary timestep can be carried out using the following distribution, \begin{align*} \mathbf{x}_{t} \sim q(\mathbf{x}_{t} | \mathbf{x}_{0}) = \mathcal{N} (\mathbf{x}_{t}; \; \mu_t = \sqrt{\bar{\alpha_t}} \; \mathbf{x}_{0}, \; \Sigma_t = (1 - \bar{\alpha_t}) \mathbf{I}) \tag{5} \end{align*} Since $\beta_t$ is a hyperparameter that is fixed beforehand, we can precompute $\alpha_t$ and $\bar{\alpha_t}$ for all timesteps and use Equation 4 to sample the latent variable $\mathbf{x}_t$ in one go.

Reverse Diffusion Process

As $T \xrightarrow{} \infty$, $\bar{\alpha_t} \xrightarrow{} 0$, the distribution $q(\mathbf{x}_{T} | \mathbf{x}_0) \approx \mathcal{N}(0, \mathbf{I})$ (also called isotropic Gaussian distribution), losing all information about the original sample. Therefore if we manage to learn the reverse distribution, we can sample $\mathbf{x}_T \sim \mathcal{N}(0, \mathbf{I})$, and run the denoising process step-wise to generate a new sample.

With a small enough step size ($\beta_t \ll 1$), the reverse process has the same functional form as the forward process. Therefore, the reverse distribution can also be modeled as a unimodal diagonal Gaussian. Unfortunately, it is not straightforward to estimate $q(\mathbf{x}_{t-1}| \mathbf{x}_{t})$, as it needs to use the entire dataset (It's intractable since it requires knowing the distribution of all possible images in order to calculate this conditional probability).

Hence, we use a network to learn this Gaussian by parameterizing the mean and variance, \begin{equation*} p_\theta (\mathbf{x}_{t-1} | \mathbf{x}_{t}) = \mathcal{N} (\mathbf{x}_{t-1}; \; \mu_\theta(\mathbf{x}_{t}, t), \; \Sigma_\theta(\mathbf{x}_{t}, t)) \tag{6} \end{equation*} Apart from the latent sample $\mathbf{x}_{t}$, the model also takes time step $t$ as input. Different time steps are associated with different noise levels, and the model learns to undo these individually.

Like the forward process, the reverse process can also be set up as a Markov chain. We can write the joint probability of the sequence of samples as, \begin{equation*} p_\theta (x_{0:T}) = p(\mathbf{x}_{T}) \prod_{t=1}^T p_\theta (\mathbf{x}_{t-1} | \mathbf{x}_{t}) \tag{7} \end{equation*} Here, $p(\mathbf{x}_{T}) = \mathcal{N}(0, \mathbf{I})$ as we start training with a sample from pure noise distribution.

Training Objective (Loss function)

The forward process is fixed and it's the reverse process that we solely focus on learning. Diffusion models can be seen as latent variable models, and are similar to variational autoencoders (VAEs), where $\mathbf{x}_{0}$ is an observed variable and $\mathbf{x}_{1}, \mathbf{x}_{2}, ..., \mathbf{x}_{T}$ are latent variables.

Maximizing the variational lower bound (also called evidence lower bound ELBO) on the marginal log-likelihood forms the objective in VAEs. For an observed variable $x$ and latent variable $z$, this lower bound can be written as, \begin{align*} \log p_\theta (x) \ge \mathbf{E}_{q(z|x)} [\log p_\theta (x|z)] - \mathbf{D}_{KL} \left( q (z|x) \; || \; p_\theta(z) \right) \end{align*}

Rewriting it in the diffusion model framework we get, \begin{align*} \text{ELBO} &= \mathbf{E}_{q(\mathbf{x}_{1:T}|\mathbf{x}_{0})} [\log p_\theta (\mathbf{x}_{0}|\mathbf{x}_{1:T})] - \mathbf{D}_{KL} \left( q (\mathbf{x}_{1:T}|\mathbf{x}_{0}) \; || \; p_\theta(\mathbf{x}_{1:T}) \right) \\ &= \mathbf{E}_{q(\mathbf{x}_{1:T}|\mathbf{x}_{0})} [\log p_\theta (\mathbf{x}_{0}|\mathbf{x}_{1:T})] - \mathbf{E}_{q(\mathbf{x}_{1:T}|\mathbf{x}_{0})} \left[ \log \frac{q (\mathbf{x}_{1:T}|\mathbf{x}_{0})}{p_\theta(\mathbf{x}_{1:T})} \right] \\ &= \mathbf{E}_{q(\mathbf{x}_{1:T}|\mathbf{x}_{0})} \left[ \log \frac{p_\theta (\mathbf{x}_{0}|\mathbf{x}_{1:T}) \; p_\theta(\mathbf{x}_{1:T}) }{q (\mathbf{x}_{1:T}|\mathbf{x}_{0})} \right] \\ &= \mathbf{E}_{q(\mathbf{x}_{1:T}|\mathbf{x}_{0})} \left[ \log \frac{p_\theta (\mathbf{x}_{0:T})}{q (\mathbf{x}_{1:T}|\mathbf{x}_{0})} \right] \\ \\ &\text{Using equation 1 and 5,} \\ &= \mathbf{E}_{q(\mathbf{x}_{1:T}|\mathbf{x}_{0})} \left[ \log p(\mathbf{x}_{T}) + \sum_{t=1}^T \log \frac{p_\theta (\mathbf{x}_{t-1} | \mathbf{x}_{t})}{q (\mathbf{x}_{t}|\mathbf{x}_{t-1})} \right] \\ \\ &\text{Taking the edge case $t=1$ out,} \\ &= \mathbf{E}_{q(\mathbf{x}_{1:T}|\mathbf{x}_{0})} \left[ \log p(\mathbf{x}_{T}) + \log \frac{p_\theta (\mathbf{x}_{0} | \mathbf{x}_{1})}{q (\mathbf{x}_{1}|\mathbf{x}_{0})} + \sum_{t=2}^T \log \frac{p_\theta (\mathbf{x}_{t-1} | \mathbf{x}_{t})}{q (\mathbf{x}_{t}|\mathbf{x}_{t-1})} \right] \\ \\ &\text{Using Markov property and then Bayes’ rule we can write,} \\ &\text{$q (\mathbf{x}_{t}|\mathbf{x}_{t-1}) = q (\mathbf{x}_{t}|\mathbf{x}_{t-1}, \mathbf{x}_{0}) = \frac{ q (\mathbf{x}_{t-1}|\mathbf{x}_{t}, \mathbf{x}_{0}) \; q (\mathbf{x}_{t}|\mathbf{x}_{0})}{ q (\mathbf{x}_{t-1}, \mathbf{x}_{0})}$ and replace,} \\ \\ &= \mathbf{E}_{q(\mathbf{x}_{1:T}|\mathbf{x}_{0})} \left[ \log p(\mathbf{x}_{T}) + \log \frac{p_\theta (\mathbf{x}_{0} | \mathbf{x}_{1})}{q (\mathbf{x}_{1}|\mathbf{x}_{0})} + \sum_{t=2}^T \log \frac{p_\theta (\mathbf{x}_{t-1} | \mathbf{x}_{t}) \; q (\mathbf{x}_{t-1}|\mathbf{x}_{0})}{q (\mathbf{x}_{t-1}|\mathbf{x}_{t}, \mathbf{x}_{0}) \; q (\mathbf{x}_{t}|\mathbf{x}_{0})} \right] \\ &= \mathbf{E}_{q(\mathbf{x}_{1:T}|\mathbf{x}_{0})} \left[ \log p(\mathbf{x}_{T}) + \log \frac{p_\theta (\mathbf{x}_{0} | \mathbf{x}_{1})}{q (\mathbf{x}_{1}|\mathbf{x}_{0})} + \sum_{t=2}^T \log \frac{p_\theta (\mathbf{x}_{t-1} | \mathbf{x}_{t})}{q (\mathbf{x}_{t-1}|\mathbf{x}_{t}, \mathbf{x}_{0})} + \sum_{t=2}^T \log \frac{q (\mathbf{x}_{t-1}|\mathbf{x}_{0})}{q (\mathbf{x}_{t}|\mathbf{x}_{0})} \right] \\ &= \mathbf{E}_{q(\mathbf{x}_{1:T}|\mathbf{x}_{0})} \left[ \log p(\mathbf{x}_{T}) + \log \frac{p_\theta (\mathbf{x}_{0} | \mathbf{x}_{1})}{q (\mathbf{x}_{1}|\mathbf{x}_{0})} + \sum_{t=2}^T \log \frac{p_\theta (\mathbf{x}_{t-1} | \mathbf{x}_{t})}{q (\mathbf{x}_{t-1}|\mathbf{x}_{t}, \mathbf{x}_{0})} + \log \frac{ q (\mathbf{x}_{1}|\mathbf{x}_{0}) \; \cancel{q (\mathbf{x}_{2}|\mathbf{x}_{0})} \; ... \; \cancel{q (\mathbf{x}_{T-1}|\mathbf{x}_{0})}}{ \cancel{q (\mathbf{x}_{2}|\mathbf{x}_{0})} \; q \cancel{(\mathbf{x}_{3}|\mathbf{x}_{0})} \; ... \; q (\mathbf{x}_{T}|\mathbf{x}_{0})} \right]\\ &= \mathbf{E}_{q(\mathbf{x}_{1:T}|\mathbf{x}_{0})} \left[ \log {\color{blue}{p(\mathbf{x}_{T})}} + \log \frac{p_\theta (\mathbf{x}_{0} | \mathbf{x}_{1})}{\color{red}q (\mathbf{x}_{1}|\mathbf{x}_{0})} + \sum_{t=2}^T \log \frac{p_\theta (\mathbf{x}_{t-1} | \mathbf{x}_{t})}{q (\mathbf{x}_{t-1}|\mathbf{x}_{t}, \mathbf{x}_{0})} + \log \frac{ \color{red}{q (\mathbf{x}_{1}|\mathbf{x}_{0})}}{\color{blue}{q (\mathbf{x}_{T}|\mathbf{x}_{0})}} \right]\\ &= \mathbf{E}_{q(\mathbf{x}_{1:T}|\mathbf{x}_{0})} \left[ \log p_\theta (\mathbf{x}_{0} | \mathbf{x}_{1}) + \log {\color{blue}\frac{p(\mathbf{x}_{T})}{q (\mathbf{x}_{T}|\mathbf{x}_{0})}} + \sum_{t=2}^T \log \frac{p_\theta (\mathbf{x}_{t-1} | \mathbf{x}_{t})}{q (\mathbf{x}_{t-1}|\mathbf{x}_{t}, \mathbf{x}_{0})} \right] \\ &= \mathbf{E}_{q(\mathbf{x}_{1}|\mathbf{x}_{0})} [\log p_\theta (\mathbf{x}_{0} | \mathbf{x}_{1})] + \mathbf{E}_{q(\mathbf{x}_{T}|\mathbf{x}_{0})} \left[ \log {\frac{p(\mathbf{x}_{T})}{q (\mathbf{x}_{T}|\mathbf{x}_{0})}} \right] + \mathbf{E}_{q(\mathbf{x}_{t-1}, \mathbf{x}_{t}|\mathbf{x}_{0})} \left[ \sum_{t=2}^T \log \frac{p_\theta (\mathbf{x}_{t-1} | \mathbf{x}_{t})}{q (\mathbf{x}_{t-1}|\mathbf{x}_{t}, \mathbf{x}_{0})} \right] \\ &= \mathbf{E}_{q(\mathbf{x}_{1}|\mathbf{x}_{0})} [\log p_\theta (\mathbf{x}_{0} | \mathbf{x}_{1})] - \mathbf{D}_{KL} (q (\mathbf{x}_{T}|\mathbf{x}_{0}) \; || \; p(\mathbf{x}_{T})) - \sum_{t>1} \mathbf{E}_{q(\mathbf{x}_{t}|\mathbf{x}_{0})} \left[ \mathbf{D}_{KL} ( q (\mathbf{x}_{t-1}|\mathbf{x}_{t}, \mathbf{x}_{0}) \; || \; p_\theta (\mathbf{x}_{t-1} | \mathbf{x}_{t})) \right] \end{align*}

The objective of maximizing this lower bound is equivalent to minimizing a loss function that is its negation, \begin{align*} L_{vlb} = \underbrace{\mathbf{D}_{KL} (q (\mathbf{x}_{T}|\mathbf{x}_{0}) \; || \; p(\mathbf{x}_{T}))}_{L_{T}} + \sum_{t>1} \mathbf{E}_{q(\mathbf{x}_{t}|\mathbf{x}_{0})} [ \underbrace{\mathbf{D}_{KL} ( q (\mathbf{x}_{t-1}|\mathbf{x}_{t}, \mathbf{x}_{0}) \; || \; p_\theta (\mathbf{x}_{t-1} | \mathbf{x}_{t}))}_{L_{t-1}} ] \; \underbrace{- \mathbf{E}_{q(\mathbf{x}_{1}|\mathbf{x}_{0})} \left[ \log p_\theta (\mathbf{x}_{0} | \mathbf{x}_{1}) \right]}_{L_0} \tag{8} \end{align*}

The term $L_T$ has no trainable parameters so it's ignored during training, furthermore, as we have assumed a large enough $T$ such that the final distribution is Gaussian, this term effectively becomes zero.

$L_0$ can be interpreted as a reconstruction term (similar to VAE).

The term $L_{t-1}$ formulates the difference between the predicted denoising steps $p_\theta (\mathbf{x}_{t-1} | \mathbf{x}_{t})$ and the reverse diffusion step $q(\mathbf{x}_{t-1}|\mathbf{x}_{t}, \mathbf{x}_{0})$ (which is given as a target to the model). It is explicitly conditioned on the original sample $\mathbf{x}_{0}$ in the loss function so that the distribution $q(\mathbf{x}_{t-1}|\mathbf{x}_{t}, \mathbf{x}_{0})$ takes the form of Gaussian. \begin{align*} q (\mathbf{x}_{t-1}|\mathbf{x}_{t}, \mathbf{x}_{0}) = \mathcal{N} (\mathbf{x}_{t-1}; \; \tilde{\mu}_t(\mathbf{x}_t, \mathbf{x}_0) \; \tilde{\beta_t}) \end{align*}

But why do we need it to be Gaussian?

Since the model output, $p_\theta (\mathbf{x}_{t-1} | \mathbf{x}_{t})$ is already parameterized as a Gaussian, every KL term compares two Gaussian distributions and therefore they can be computed in closed form. This makes the loss function tractable.

Intuitively, a painter (our generative model) needs a reference image ($\mathbf{x}_{0}$) to slowly draw (reverse diffusion step $q(\mathbf{x}_{t-1} | \mathbf{x}_t)$) an image. Thus, we can take a small step backward, meaning from noise to generate an image, if and only if we have $\mathbf{x}_{0}$ as a reference.

Using Bayes' rule we can write, \begin{align*} q (\mathbf{x}_{t-1}|\mathbf{x}_{t}, \mathbf{x}_{0}) &= q (\mathbf{x}_{t}|\mathbf{x}_{t-1}, \mathbf{x}_{0}) \; \frac{q (\mathbf{x}_{t-1}|\mathbf{x}_{0})}{q (\mathbf{x}_{t}| \mathbf{x}_{0})} \\ \\ &\text{Using equation 2 and 4,} \\ &= \mathcal{N} (\mathbf{x}_t; \; \sqrt{1 - \beta_t} \; \mathbf{x}_{t-1}, \; \beta_t \mathbf{I}) \; \frac{ \mathcal{N} (\mathbf{x}_{t-1}; \; \sqrt{\bar{\alpha}_{t-1}} \; \mathbf{x}_{0}, \; (1 - \bar{\alpha}_{t-1}) \mathbf{I})}{ \mathcal{N} (\mathbf{x}_{t}; \; \sqrt{\bar{\alpha}_{t}} \; \mathbf{x}_{0}, \; (1 - \bar{\alpha}_{t}) \mathbf{I})} \\ \\ &\text{Replacing $1 - \beta_t = \alpha_t$,} \\ &= \mathcal{N} (\mathbf{x}_t; \; \sqrt{\alpha_t} \; \mathbf{x}_{t-1}, \; \beta_t \mathbf{I}) \; \frac{ \mathcal{N} (\mathbf{x}_{t-1}; \; \sqrt{\bar{\alpha}_{t-1}} \; \mathbf{x}_{0}, \; (1 - \bar{\alpha}_{t-1}) \mathbf{I})}{ \mathcal{N} (\mathbf{x}_{t}; \; \sqrt{\bar{\alpha}_{t}} \; \mathbf{x}_{0}, \; (1 - \bar{\alpha}_{t}) \mathbf{I})} \\ & \propto \text{exp} \left[ -\frac{1}{2} \left( \frac{(\mathbf{x}_t - \sqrt{\alpha_t} \; \mathbf{x}_{t-1})^2}{\beta_t} + \frac{(\mathbf{x}_{t-1} - \sqrt{\bar{\alpha}_{t-1}} \; \mathbf{x}_{0})^2}{(1 - \bar{\alpha}_{t-1})} - \frac{(\mathbf{x}_{t} - \sqrt{\bar{\alpha}_{t}} \; \mathbf{x}_{0})^2}{(1 - \bar{\alpha}_{t})} \right) \right] \\ &= \text{exp} \left[ -\frac{1}{2} \left( \frac{\mathbf{x}_t^2 + \alpha_t \; \mathbf{x}_{t-1}^2 - 2 \; \mathbf{x}_t \sqrt{\alpha_t} \; \mathbf{x}_{t-1}}{\beta_t} + \frac{\mathbf{x}_{t-1}^2 + \bar{\alpha}_{t-1} \; \mathbf{x}_{0}^2 - 2\; \mathbf{x}_{t-1} \sqrt{\bar{\alpha}_{t-1}} \; \mathbf{x}_{0}}{(1 - \bar{\alpha}_{t-1})}- \frac{(\mathbf{x}_{t} - \sqrt{\bar{\alpha}_{t}} \; \mathbf{x}_{0})^2}{(1 - \bar{\alpha}_{t})} \right) \right] \\ &= \text{exp} \left[ -\frac{1}{2} \left( \mathbf{x}_{t-1}^2 \left( \frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}_{t-1}} \right) + \mathbf{x}_{t-1} \left( \frac{- 2 \; \mathbf{x}_t \sqrt{\alpha_t}}{\beta_t} + \frac{- 2\; \sqrt{\bar{\alpha}_{t-1}} \mathbf{x}_0}{1 - \bar{\alpha}_{t-1}} \right) + C(\mathbf{x}_t, \mathbf{x}_0)) \right) \right] \\ \\ &\text{where C is a function whose details are omitted for readability.} \\ &= \text{exp} \left[ -\frac{1}{2} \left( \mathbf{x}_{t-1}^2 \left( \frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}_{t-1}} \right) - 2 \; \mathbf{x}_{t-1} \left( \frac{\mathbf{x}_t \sqrt{\alpha_t}}{\beta_t} + \frac{\sqrt{\bar{\alpha}_{t-1}} \mathbf{x}_0}{1 - \bar{\alpha}_{t-1}} \right) + C(\mathbf{x}_t, \mathbf{x}_0)) \right) \right] \\ \\ &\text{which can be written in the form,} \\ &= \text{exp} \left[ -\frac{1}{2} \left( \frac{(\mathbf{x}_{t-1} - \tilde{\mu}_t(\mathbf{x}_t, \mathbf{x}_0))^2}{\tilde{\beta}_t} \right) \right] \end{align*}

Such that the variance is, \begin{align*} \tilde{\beta_t} &= \left( \frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}_{t-1}} \right)^{-1} = \frac{(1 - \bar{\alpha}_{t-1}) \; \beta_t }{\alpha_t - \alpha_t \; \bar{\alpha}_{t-1} + \beta_t} = \frac{(1 - \bar{\alpha}_{t-1}) \beta_t }{1 - \alpha_t \; \bar{\alpha}_{t-1} } \\ &= \frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_{t}} \; \beta_t \tag{9} \end{align*}

and the mean is, \begin{align*} \tilde{\mu}_t(\mathbf{x}_t, \mathbf{x}_0) &= \left( \frac{\mathbf{x}_t \sqrt{\alpha_t}}{\beta_t} + \frac{\sqrt{\bar{\alpha}_{t-1}} \mathbf{x}_0}{1 - \bar{\alpha}_{t-1}} \right) \; \left( \frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}_{t-1}} \right)^{-1} \\ &= \frac{\sqrt{\alpha_t} \; (1 - \bar{\alpha}_{t-1}) \; \mathbf{x}_t + \beta_t \; \sqrt{\bar{\alpha}_{t-1}} \; \mathbf{x}_0 }{\alpha_t - \alpha_t \; \bar{\alpha}_{t-1} + \beta_t} \\ &= \frac{\sqrt{\alpha_t} \; (1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_{t}} \mathbf{x}_t + \frac{\beta_t \; \sqrt{\bar{\alpha}_{t-1}}}{1 - \bar{\alpha}_{t}} \; \mathbf{x}_0 \end{align*}

Equation 4 is $\mathbf{x}_t = \sqrt{\bar{\alpha_t}} \; \mathbf{x}_{0} + \sqrt{1 - \bar{\alpha_{t}}} \; \epsilon_t$, which can be rewritten as, $\mathbf{x}_{0} = \frac{\mathbf{x}_t - \sqrt{1 - \bar{\alpha_{t}}} \; \epsilon_t}{\sqrt{\bar{\alpha_t}}}$. Substituting, \begin{align*} \tilde{\mu}_t &= \frac{\sqrt{\alpha_t} \; (1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_{t}} \mathbf{x}_t + \frac{\beta_t \; \sqrt{\bar{\alpha}_{t-1}}}{1 - \bar{\alpha}_{t}} \; \frac{\mathbf{x}_t - \sqrt{1 - \bar{\alpha_{t}}} \; \epsilon_t}{\sqrt{\bar{\alpha_t}}} \\ &= \frac{\sqrt{\alpha_t} \; (1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_{t}} \mathbf{x}_t + \frac{\beta_t}{1 - \bar{\alpha}_{t}} \; \frac{\mathbf{x}_t - \sqrt{1 - \bar{\alpha_{t}}} \; \epsilon_t}{\sqrt{\alpha_t}} \\ &= \frac{ \left( \alpha_t \; (1 - \bar{\alpha}_{t-1}) + \beta_t \right) \mathbf{x}_t - \beta_t \sqrt{1 - \bar{\alpha_{t}}} \; \epsilon_t }{\sqrt{\alpha_t} \; (1 - \bar{\alpha_{t}})} \\ &= \frac{ \left( 1 - \bar{\alpha_{t}} \right) \mathbf{x}_t - \beta_t \sqrt{1 - \bar{\alpha_{t}}} \; \epsilon_t }{\sqrt{\alpha_t} \; (1 - \bar{\alpha_{t}})} \\ &= \frac{1}{\sqrt{\alpha_t}} \left( \mathbf{x}_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha_{t}}}} \; \epsilon_t \right) \tag{10} \end{align*}

Therefore, the term $L_{t-1}$ estimates the KL-divergence between, \begin{align*} \text{Predicted: } & p_\theta (\mathbf{x}_{t-1} | \mathbf{x}_{t}) = \mathcal{N} (\mathbf{x}_{t-1}; \; \mu_\theta(\mathbf{x}_{t}, t), \; \Sigma_\theta(\mathbf{x}_{t}, t))\\ \text{Target: } & q (\mathbf{x}_{t-1}|\mathbf{x}_{t}, \mathbf{x}_{0}) = \mathcal{N} (\mathbf{x}_{t-1}; \; \tilde{\mu}_t(\mathbf{x}_t), \; \tilde{\beta_t}) \\ \end{align*}

Recall that we learn a neural network that predicts the mean and diagonal variance of the Gaussian distribution of the reverse process. Ho et al. decided to keep the predicted variances fixed to time-dependent constants because they found that learning them leads to unstable training and poorer sample quality. They set $\Sigma_\theta(\mathbf{x}_{t}, t) = \sigma_t^2 \; \mathbf{I}$, where $\sigma_t^2 = \beta_t$ or $\tilde{\beta}_t$ (both gave same results).

Because $\mathbf{x}_t$ is available as input at training time, instead of predicting the mean (equation 10), we make it predict the noise term $\epsilon_t$ using $\epsilon_\theta$. We can then write the predicted mean as, \begin{align*} \mu_\theta(\mathbf{x}_{t}, t) = \frac{1}{\sqrt{\alpha_t}} \left( \mathbf{x}_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha_{t}}}} \; \epsilon_\theta(\mathbf{x}_{t}, t) \right) \tag{11} \end{align*}

and the predicted de-noised sample can be written using the reparameterization trick as, \begin{align*} \mathbf{x}_{t-1} &= \mu_\theta(\mathbf{x}_{t}, t) + \sqrt{\Sigma_\theta(\mathbf{x}_{t}, t)} \; z_t \\ &= \frac{1}{\sqrt{\alpha_t}} \left( \mathbf{x}_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha_{t}}}} \; \epsilon_\theta(\mathbf{x}_{t}, t) \right) + \sigma_t z_t \tag{12} \end{align*} where $z \sim \mathcal{N}(0, 1)$ at each time step.

Thus, the network predicts only the noise term at each time step $t$. Let's simplify the term $L_{t-1}$, given that the variances are equal. KL-divergence b/w two Gaussians is given as:, \begin{align*} D_{KL}(p||q) = \frac{1}{2}\left[\log\frac{|\Sigma_q|}{|\Sigma_p|} - k + (\mu_p-\mu_q)^T\Sigma_q^{-1}(\mu_p-\mu_q) + tr\left\{\Sigma_q^{-1}\Sigma_p\right\}\right] \end{align*} where $k$ is number of dimensions.

\begin{align*} L_{t-1} &= \mathbf{D}_{KL} ( q (\mathbf{x}_{t-1}|\mathbf{x}_{t}, \mathbf{x}_{0}) \; || \; p_\theta (\mathbf{x}_{t-1} | \mathbf{x}_{t})) \\ &= \frac{1}{2}\left[- k + \frac{ (\tilde{\mu}_t - \mu_\theta(\mathbf{x}_{t}, t)) (\tilde{\mu}_t - \mu_\theta(\mathbf{x}_{t}, t))^T }{\sigma_t^2} + tr\left\{\mathbf{I} \right\}\right] \\ &= \frac{1}{2}\left[- k + \frac{ (\tilde{\mu}_t - \mu_\theta(\mathbf{x}_{t}, t)) (\tilde{\mu}_t - \mu_\theta(\mathbf{x}_{t}, t))^T }{\sigma_t^2} + k \right] \\ &= \frac{1}{2 \sigma_t^2} || \tilde{\mu}_t - \mu_\theta(\mathbf{x}_{t}, t) ||^2 \\ &= \frac{1}{2 \sigma_t^2} \Vert \frac{1}{\sqrt{\alpha_t}} \left( \mathbf{x}_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha_{t}}}} \; \epsilon_t \right) - \frac{1}{\sqrt{\alpha_t}} \left( \mathbf{x}_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha_{t}}}} \; \epsilon_\theta(\mathbf{x}_{t}, t) \right) \Vert^2 \\ &=\frac{\beta_t^2}{2 \sigma_t^2 \; \alpha_t \; (1 - \bar{\alpha_{t}}) } || \epsilon_t - \epsilon_\theta(\mathbf{x}_{t}, t) ||^2 \tag{13} \end{align*} The objective reduces to a weighted L2-loss between the noises and second term of the loss function becomes, $\mathbf{E}_{q}[L_{t-1}] = \mathbf{E}_{\mathbf{x}_{t}, \epsilon_t} [w_t \; || \epsilon_t - \epsilon_\theta(\mathbf{x}_{t}, t) ||^2 ]$

Empirically, Ho et al. found that training the diffusion model works better with a simplified objective that ignores the weighting term in $L_{t-1}$. They also got rid of the term $L_0$ by altering the sampling method, such that at the end of sampling ($t$ = 1), we obtain $\mathbf{x}_0 = \mu_\theta(\mathbf{x}_0, t=1)$.

The simplified loss function for DDPM is given as, \begin{align*} L_{simple} &= \mathbf{E}_{\mathbf{x}_{t}, \epsilon_t} \left[|| \epsilon_t - \epsilon_\theta(\mathbf{x}_{t}, t) ||^2 \right] \tag{14.1} \\ &= \mathbf{E}_{\mathbf{x}_{0}, \epsilon_t} \left[|| \epsilon_t - \epsilon_\theta(\sqrt{\bar{\alpha_t}} \; \mathbf{x}_{0} + \sqrt{1 - \bar{\alpha_{t}}} \; \epsilon_t, t) ||^2 \right] \tag{14.2} \end{align*}

The training and sampling algorithms in the DDPM paper (Ho et al.)

Credits: While writing this blog, I have referred to Lillian Weng's blog post, AI Summer's post and Luo at al. (2022)