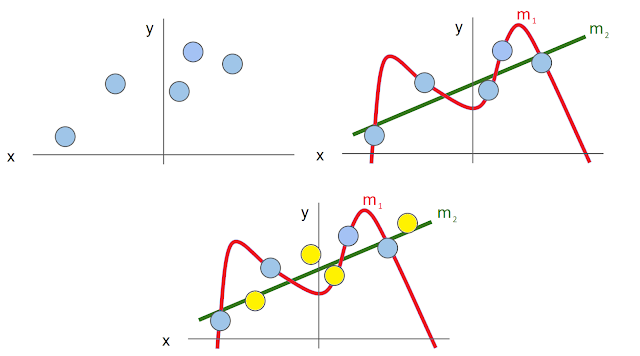
Data Manipulation for Deep Learning
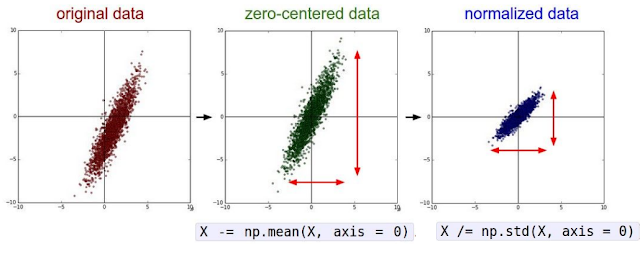
Datasets drive our choices for all the deep learning hyperparameters and peculiarities involved in making accurate predictions. We split the dataset into a training set, test set, and validation set. Our model is trained on the training set, and we choose the hyperparameters (usually by trial and error) on the validation set. We select the hyperparameters that have the highest accuracy on the validation set and then fix our model. The test set is reserved to be used only once at the very end of our pipeline to evaluate our model. Our algorithm is run exactly once on the test set and that accuracy gives us a proper estimate of our model's performance on truly unseen data. Now that we have created our training set to perform the optimization process, let's look at how manipulating this data can help us train our model. Data Preprocessing The loss function is computed on the mini-batch of the training data at every step of the optimization algorithm. Therefore, the loss ...