Markov Decision Processes Part 3: Bellman Equations and Optimal Policy

Since two posts we have been talking about MDPs. As discussed in the previous post, the ultimate goal of a MDP is to maximize the total future reward. In the last post, we had calculated the cumulative sum of the long-term rewards (Gt). In this post, we will calculate the expected long-term reward which the agent has to maximize. 

A value of a state is the total amount of reward an agent can expect to accumulate over the future, starting from that state. A value function computes the value of a state. A value of state gives us an estimate of how good the state is to be in. The value of a state should not be confused with rewards. A reward signal indicates what is good in an immediate sense, whereas a value function specifies what is good in the long run. For example, a state might always yield a low immediate reward but still have a high value because it is regularly followed by other states that yield high rewards. Since our goal is to maximise long-term reward, we take into account the value function. We then seek actions that bring about states of the highest value, not the highest reward because these actions obtain the greatest amount of reward for us over the long run. The value function vπ of a state s under a policy π is given by,

Note that the value of Gt is same as the one computed in the previous post and we are simply written down an expression for its expected value.  In order to solve this, we use the Bellman equation,
As discussed earlier, the value of a state determines how good is a state for an agent to be in. An optimal policy is the one which maximizes the total sum of rewards. Therefore, an optimal policy would always suggest an action in a particular state in the direction of increasing value. For example if an agent is in a state s with a value 0.51 and an action up will result in state s1 (value = 0.2), action down will result in state s2 (value = 0.31), action left will result in state s3 (value = 0.7) and action right will result in state 4 (value = 0.36); an optimal policy would always suggest the action left. An optimal policy would always drive an agent towards the increasing value of a state. The state value function for an optimal policy can be computed using,
Similarly, we can also define the value of taking an action a in the state s under the policy π using an action-value function. An action-value function computes the expected reward an agent would gain in the long term after executing action a in the state s. It is given by,


In order to solve this, we use the Bellman equation,

Once we have computed the value of each action, we can intuitively select the action with the highest value, because that action will result in the highest total reward in the long-run. Therefore, an optimal policy would always suggest the action with the highest qπ  value. 

As discussed above, an optimal value will always select an action that yields the highest long-term reward or in other words, the action that has the highest qπ value.

In conclusion, the optimal policy will be related to the value functions as follows:
References: 
1. CS188 Introduction to Artificial Intelligence, UCB
2. Sutton, R. S., & Barto, A. G. (2018). Reinforcement learning: An introduction. MIT press.

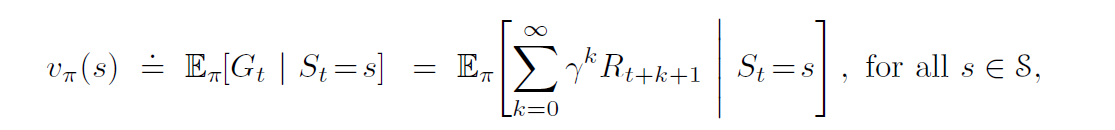
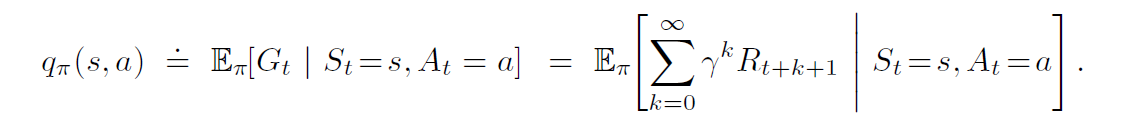
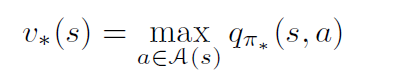
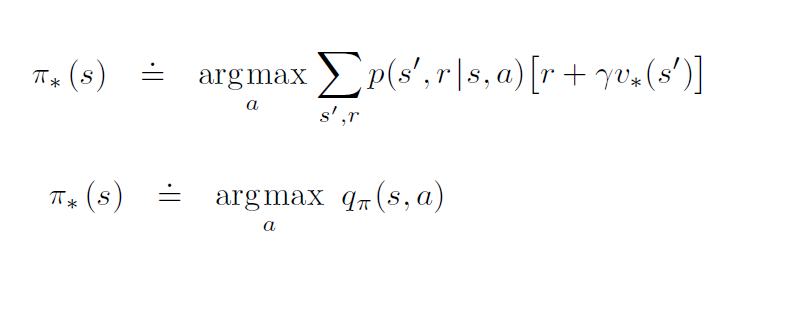
Comments

Post a Comment

Popular posts from this blog

The move_base ROS node

Image
move_base package provides the move_base node which is a major element of ROS Navigation stack. It moves the robot from its current position to a goal position. When path planning is done, the user gives uses the 2D Nav Goal in RVIZ to specify the goal position and orientation. This position (x,y,z) and orientation(x,y,z,w) are actually published in move_base/goal topic. The move_base node links together a global and local planner to accomplish its global navigation task. The Global Planner It is in charge of calculating the safe path in order to arrive at goal pose. Note that the path is calculated before the robot starts moving so it will not take into account the laser readings while moving i.e. unscanned obstacles that are not in the map. Navfn Planner The Navfn planner is the most commonly used global planner for ROS Navigation. It uses Dijkstra's algorithm in order to calculate the shortest path between the initial pose and the goal pose. Carrot Planner This plann
Read more

Three Wheeled Omnidirectional Robot : Motion Analysis

Image
A Three-wheeled omnidirectional robot is capable to moving in any given direction without rotating by giving velocities to the three wheels in a certain ratio. All motors are situated at an angle of 120 degrees from each other. f B ,  f L ,  f R  are for back , left and right wheel respectively. a x  and a y  are accelerations in X R  and Y R  axis in Robot frame and w is the angular velocity in Robot frame. Hence putting the values of alpha and making it into a matrix form we get : As we need to obtain the f values, we will invert the matrix. We need  a x  , a y  and w is the world frame, so we apply transformation. The transformation angle is    α 1  = 30 degrees.  Putting this in the previous equation, Multiplying the two matrices, we get the final relation as : For example, if you want to move the robot along X axis(world frame), put  a x W  = 1 , a y W  = 0 , w = 0 You will get the ratio of velocities as : 1 : -2 : 1 .
Read more

Dijkstra`s Algorithm vs A* Algorithm

Image
In order to find the shortest path, the two well-known algorithms that are used widely in the field of robotics are the Dijkstra`s Algorithm and the A* Algorithm. In Dijkstra's algorithm, we calculate the weight of the adjacent nodes and then visit the node that has the least weight. This process is continued until the goal node is reached. Djikstra`s algorithm becomes very similar to the Grassfire Algorithm in case of grids where the weight of each iteration is equal to 1. In such cases, we end up visiting all the nodes until the goal node is reached. This makes it very difficult to use it on larger grids because we visit all the unnecessary nodes.  Whereas the A* algorithm uses the concept of a Heuristic function. In this algorithm, we visit only the nodes that can be on the shortest path by finding the distance of the adjacent nodes to the goal node and choosing the node that is the closest.
Read more