Markov Decision Processes Part 1: Basics

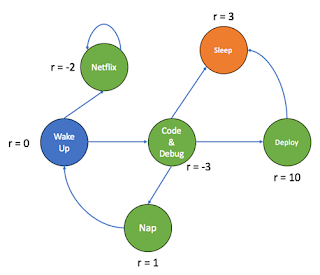
We are always solving MDPs in the back of our minds. Should I sleep right now? Should I watch Netflix? Should I code? We generally weigh our options based on returns or what is called rewards in MDPs. We always work towards gaining the highest long-term reward possible. If I watch Netflix, I loose on the hours when I could have slept or deployed by application (so negative reward). If I deploy my application, I could make more money(greater positive reward). If I sleep or take a nap, I am improving my health(a lesser positive reward). And that's exactly what a MDP is!

  

The word "Markov" means that the action-outcome depends only on the current state that an agent is in. It is independent of the future or past states. Therefore, the next state will only be dependent on the current state. The basic framework of a MDP is defined below :

• States: S
• Actions: A(s)
• Model : T(s,a,s') ~ P(s' | s,a)
• Reward: R(s)

--------------------------------------------

          Policy: π(s) = a

Let's take an example to understand each component separately. Consider a grid world shown in the figure below. This is a very common example which you would see in almost all MDP explanations. The grid is a 3*4 table with 12 boxes. A robot starts from the "start" position marked by (1,1). The end goal of the robot is to reach the grid (3,4).

Formalizing a MDP in this problem, it is pretty straightforward to say that each box represents a particular state that the robot could be in. The box (2,2) is blocked therefore the robot cannot be in that position, so it is not a state. Hence, the number of states = 11.

States:  (1,1),(1,2)........(3,4) expect (2,2).

Now that we have defined the states, we will talk about how a robot can change a particular state. If a robot in a state/box, it can go up, down, right and left. These form our actions that a robot can perform in order to change its state. For example, if the robot's current state s = (1,1) it can perform action "up" to reach the state s' = (2,1).

Actions: Up, Down, Right, Left.

A model or a transition model is a function of three variables, the current state s, an action a, and the state s' which can be achieved by performing action a in the state s. So, a model basically tells you what will happen when you carry out action a in a state s. The function p(s'| s,a) defines the dynamics of the MDP.

To understand this better we need to define to disparate worlds: deterministic world and stochastic world.  In a deterministic world, the actions are deterministic, i.e. if an action "up" is carried out, the agent will irrefutably go up. For example, if the robot is in (1,3) state and action "up" is carried out, the robot will move to the state (2,3) with a probability 1. On the other hand, in a stochastic world, the actions have a probability distribution and the probabilities add up to 1. In a stochastic world, if a robot at state (1,3) performs action "up", there is a 80% chance that the robot will move to state (2,3) [action up], 10% chance that it will move to (1,2) [action left] and 10% chance that it will move to (4,1) [action right].

In reinforcement learning, the purpose or goal of the agent is formalized in terms of a special signal, called the reward, passing from the environment to the agent. In our example we want the robot to reach the state (3,4), hence the reward of +1 is given to that state; this lures the robot to that state. On the other hand, we strictly want our robot to state away from the state (2,4) and therefore we give a reward of -1 to that state. Positive rewards encourage the robot to move towards itself, whereas negative rewards encourage the robot to stay away from itself. Furthermore, we give a reward of -0.1 at each step prior to the escape; this exhorts the robot to exit the grid as quickly as possible(exiting means reaching the state (3,4)).

If we want an agent to do something for us, we must provide rewards to it in such a way that in maximizing them the agent will also achieve our goals. Moreoever, a chess-playing agent should

be rewarded only for actually winning, not for achieving subgoals such as taking its

opponent’s pieces or gaining control of the centre of the board. It might find a way to take the opponent’s pieces even at the cost of losing the game. The reward signal is your way of communicating to the robot what you want it to achieve, not how you want it achieved.

A solution to a MDP is called a policy. A policy takes the current state of the robot as an input and returns an action that the robot should take. For example, a uniform random policy would uniformly select a random action. Say the current state of the robot is (1,1). A uniform random policy would suggest the robot to move up 50% of the time and move right another 50% of the time. (Think of it as head and tails). Of all the policies that can be possible, an optimal policy is a policy that maximizes long-term expected reward. Denoted by π*, an optimal policy is the best solution of a MDP. For example, an optimal policy would always suggest a robot at state (3,3) to move right. Furthermore, it would never suggest a robot at state (2,3) to move right (because of the negative reward). Optimal policies are usually deterministic so you do not need to worry about the uncertainty mentioned above.

References: 

1. CS188 Introduction to Artificial Intelligence, UCB

2. Sutton, R. S., & Barto, A. G. (2018). Reinforcement learning: An introduction. MIT press.