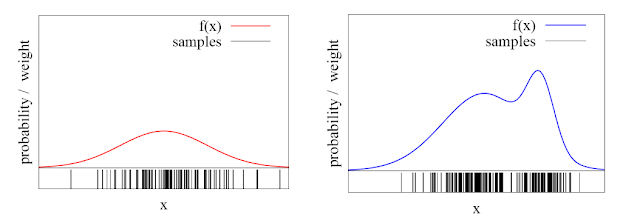
Occupany Grid Mapping
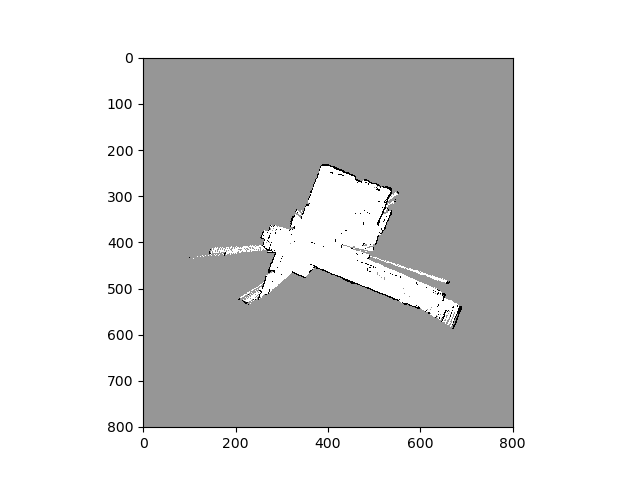
In order to map out an unknown environment for future reference, a robot uses the Simultaneous Localization And Mapping (SLAM) algorithm. We talked about solving the localization problem using Filtering in the previous posts. In this post, we will look at the mapping problem. We will assume that we know the position/orientation of the robot in the 3D world (which we obtain from filtering), and want to build a map of the objects in the world. Occupancy grid map (OGM) is a very common way of representing the layout of the unknown environment. It is a large gray-scale image where each pixel represents a cell in the physical world. The cells that are occupied are colored black and empty cells represent free space are colored white. The grey cells represent unexplored areas. Before moving forward, lets make some assumptions: Assumption 1: each cell is either free or occupied. We model each cell as a binary random variable that indicates occupancy. Let the probability that the cell ...